I trained a multi-class classifier on images of cats, dogs and wild animals and passed an image of myself, it’s 98% confident I’m a dog. The problem isn’t that I passed an inappropriate image, because models in the real world are passed all sorts of garbage. It’s that the model is overconfident about an image far away from the training data. Instead we expect a more uniform distribution over the classes. The overconfidence makes it difficult to post-process model output (setting a threshold on predictions, etc.), which means it needs to be dealt with by the architecture.
In this post I explore a Bayesian method for dealing with overconfident predictions for inputs far away from training data in neural networks. The method is called last layer Laplace approximation (LLLA) and was proposed in this paper published in ICML 2020.
Why is this a problem?
You might argue that since I only trained the classifier on animals, of course it breaks when you show it a human, and you’re right. However, in real world systems, we aren’t able to filter out animal images from non-animal images before sending it to the model, so we need it to be robust to garbage input. The animal-human example tries to replicate this on a small scale (one image). Properly quantifying uncertainty is important because we (as practitioners training the models) can’t be confident in the model’s ability to generalize if it assigns arbitrarily high confidence to garbage input.
Softmax Classifier
The 3-class classifier was trained on images of cats, dogs and wild animals taken from Kaggle that can be downloaded here.

The model used was Resnet-18, which yields ~99% accuracy on the validation set. Only using this for evaluation would have us believe it’s an amazing model, but that’s not why we’re here. Below is the image of myself and a dog, where apparently I’m more dog than this actual dog. Even worse, it’s 98% confident that I’m a dog, so I’d be a dog even if we were only considering predictions with over 95% confidence.

Parsed an image of myself through the animal network and it's 98% confident I'm a dog.
Possible Solutions
This paper proposes a nice explanation and proof for the over-confidence of out-of-distribution examples in ReLU networks. Essentially, they prove that for a given class $k$, there exists a scaling factor $\alpha > 0$ such that the softmax value of input $\alpha x$ as $\alpha \to \infty$ is equal to 1. This means that there are infinitely many inputs that obtain arbitrarily high confidence in ReLU networks. A bi-product of which is the inability to set softmax thresholds to preserve classifier precision.
There are a couple of ways to approach this, which broadly fall into two categories: 1) building a generative model for the data (VAE, GAN, etc.) or 2) changing the structure of the network. The generative approach doesn’t really solve the problem with ReLU networks. There’s a great Chicken-MNIST blog post that discusses a potential solution using VAEs. Another approach, that would fall into the category of changing the network structure is to change the loss function, which was done in this paper. Instead, we’ll opt for changing the network by putting a posterior over the weights of the last layer, as decsribed in this paper.
Last Layer Bayesian-ness
Bayesian methods are great for quantifying uncertainty, and that’s what we want in this case. The problem is that this model, and all other deep learning models, have way too many parameters to have an appropriate posterior over all. The proposed solution is to only have a posterior over the weights in the last layer. This is perfect for implementation because we can in theory have the best of both worlds - first use the ReLU network as a feature extractor, then a Bayesian layer at the end to quantify uncertainty.
The posterior over the last layer weights can be approximated with a Laplace approximation and can be easily obtained from the trained model with Pytorch autograd.
Amazingly, the only parameter we have to focus on is $\sigma^2_0$, the variance of the prior on the weights. It governs how conservative the predictions are. As $\sigma^2_0$ increases, the confidence of out-of-distribution predictions decreases, which is what we want. However we cannot naively increase $\sigma^2_0$ as making it too large would cause predictions for images close to the training data to be uniform as well. Decreasing $\sigma^2_0$ causes the predictions to be more and more similar to the softmax predictions. We want a balance between the two extremes.
Now we can use the last layer Laplace approximation to see if it helps the overconfidence issue. Below I ran the same images of myself and the dog through both the model using softmax and last layer Laplace. I’m still a dog, but with much lower confidence, allowing us to potentially set a threshold on the output.

Comparison of outputs from using LLLA and Softmax. The scores seem to be muted with LLLA, so we have to explore whether this happens across the board or only for one image.
Animal Model + Animal Data
So far we’ve only tested the method with two hand selected images. I want to see if this method just scales down all confident predictions, or if it is doing some interesting stuff under the hood. To start more evaluation, we’ll plot the confidence level of the top class for the validation data (all animal images, no garbage).
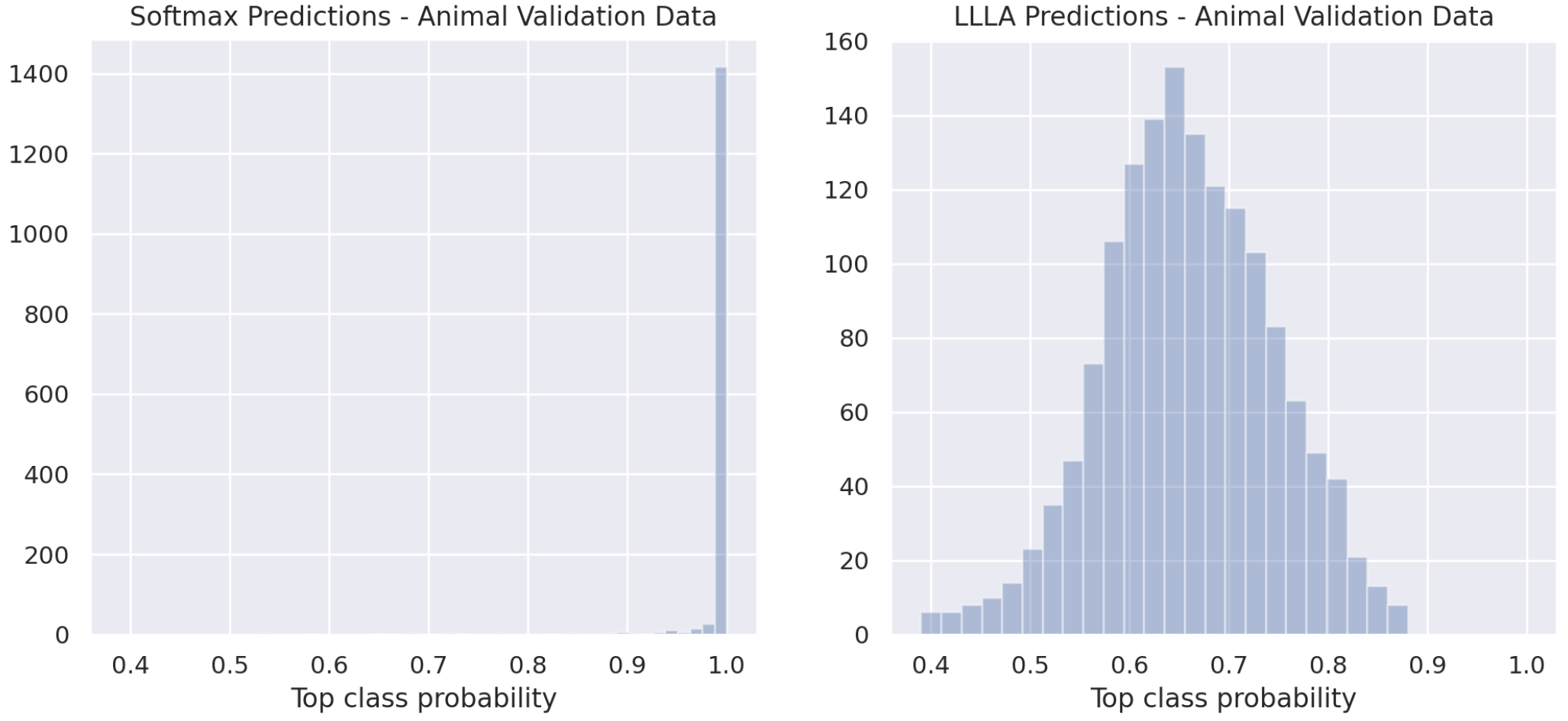
Comparison of the top class score for the animal data test set using LLLA and Softmax. There are no out-of-distribution images here, so it's difficult to say how concerning this is.
The softmax model is really confident about nearly all the images in the validation set, whereas the LLLA model has a flatter confidence distribution. Can’t stop now! When does the LLLA model produce high or low confidence predictions?
It’s difficult to come to a general conclusion on this, but interestingly the LLLA model can produce predictions with both high and low confidence even when the softmax prediction confidence is high.


Animal Model + Simpsons Data
Last thing - what’s the confidence distribution for images that are completely different. This should give us a proxy for how both methods deal with complete garbage thrown at them. As discussed before, this is the problem ML models in the wild face - you train them to learn specific patterns and send them into the deep end where they have to deal with completely unseen data.

I passed 300 of these Simpsons character faces into the classifier and plotted the confidence level of the top class for both LLLA and softmax models. Again, since these are garbage images, we’d expect this distribution to be closer to $0.33$ (random chance). Keep in mind the confidence will never drop below $0.33$ as we’re only looking at the top class.
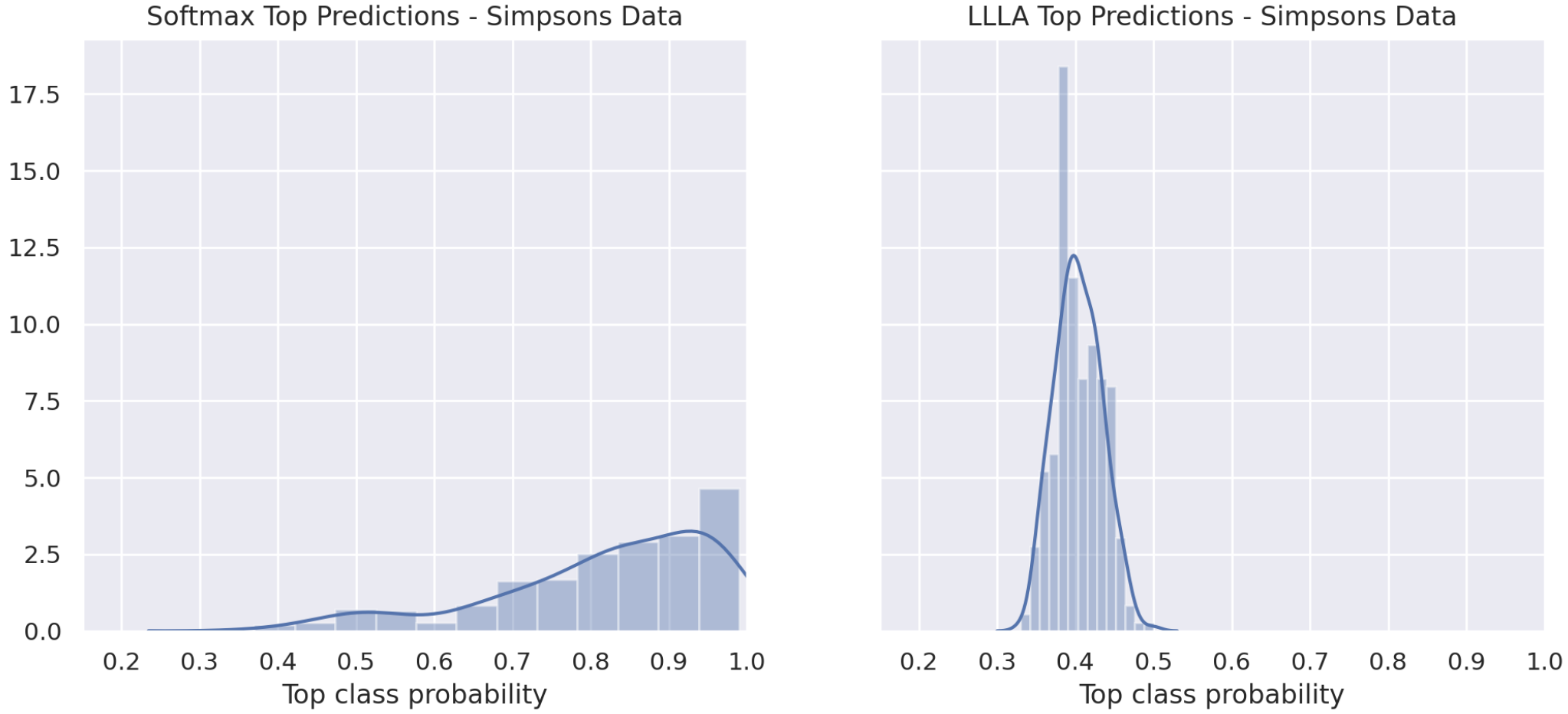
Distribution of top-class scores (probabilities) using Simpsons characeters on our animal classifier. This plot is concerning as many of Simpsons characters have been predicted as an animal with high probability. The LLLA scores (right) here are much more reasonable.
These results are pretty alarming for the softmax classifier. The majority of Simpson faces are predicted as cat/dog/wild with probability greater than $0.8$ with the softmax classifier, whereas there are no predictions with greater than $0.5$ confidence from the LLLA classifier. This is amazing!
Confidence Threshold
All of this would be for nothing if the model metrics aren’t preserved after post-processing the output. The simplest way to test this is to examine the tradeoff between a confidence threshold and model accuracy. I’ve taken the validation set, which are appropriate inputs for the classifier, and plotted the model accuracy at different thresholds.
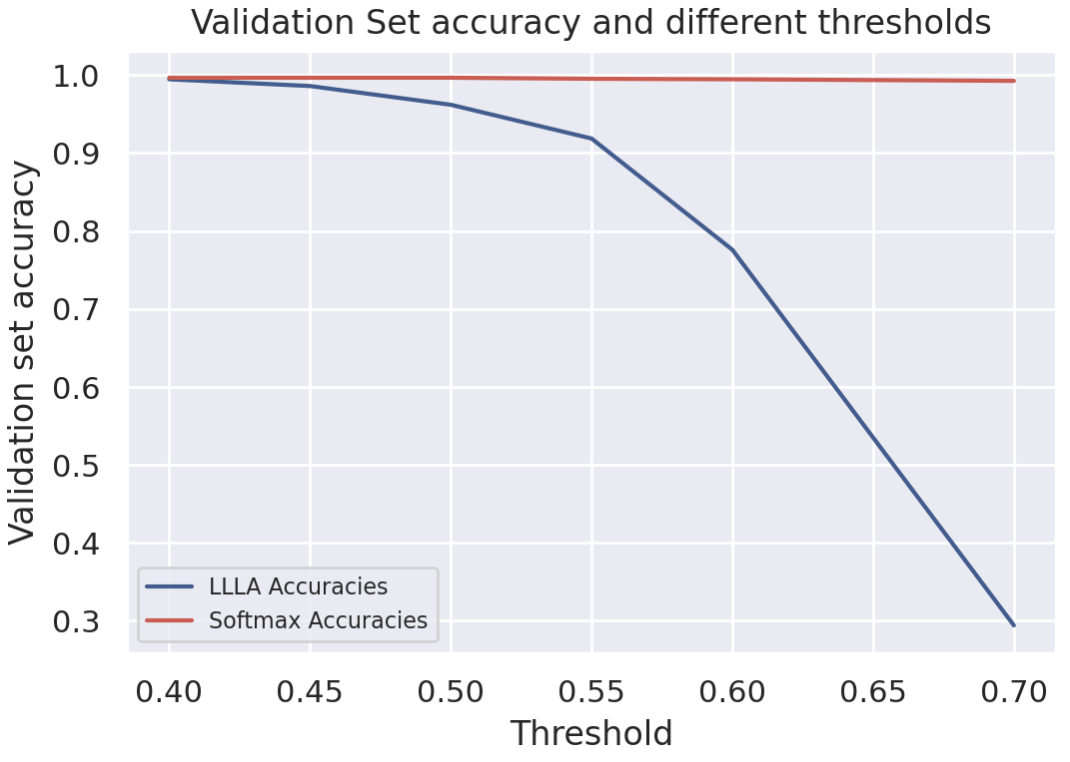
Even with a threshold value of $0.5$, the LLLA model is more than 95% accurate on the validation set. In addition, using the $0.5$ threshold with the LLLA model excludes all Simpsons characters discussed in the previous section, whereas the softmax model will be mostly unchanged.
Conclusion
From the light experimentation done here, the last layer Laplace approximation seems to be a good solution to the overconfidence problem. Of course its usage will depend on the specific problem and allowable tradeoff between precision and recall for each class, however these results are promising nonetheless. The icing on the LLLA cake is its ease of implementation and seamless integration with transfer learning.
All the code used in this blog can be found here.